|
Intervalles ouverts centrés
Considérons un intervalle ouvert quelconque.
]a,b[ = {x ∈ R : a < x < b}

Recherchons le milieu (ou centre) c de cet intervalle. Il est obtenu par  . .
Le rayon r de l'intervalle est alors la distance entre le centre et les "bords" (on parle de bornes) a et b de l'intervalle.
r est donc un réel strictement positif.
r=c-a

Plus simplement, c'est donc aussi la largeur (le diamètre) de l'intervalle divisé par 2.
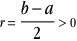
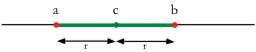
Exprimer l'appartenance d'un réel x à l'intervalle équivaut donc à dire que la distance entre x et le centre de l'intervalle doit être inférieure au rayon.
x ∈ ]a,b[⇔ d(x,c)<r⇔|x-c|<r
On peut aussi obtenir cette relation de la manière suivante:
x ∈ ]a,b[
⇔
a<x<b
⇔
0<x-a et x-b< 0
⇔
0<x-(c-r) et x-(c+r)<0
⇔
-r<x-c et x-c<r
⇔
-r<x-c<r
⇔
|x-c|<r
exemple 1: on considère l'intervalle ouvert 
recherchons le centre et le rayon:
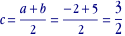

l'intervalle 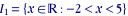 peut donc être défini de manière équivalente par peut donc être défini de manière équivalente par
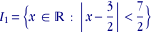

exemple 2: soit l'intervalle défini par 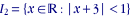
la condition d'appartenance à l'intervalle étant |x-(-3)|<1, nous voyons que le rayon est égal à 1 et le centre est -3.
c=-3
r=1
les bornes de l'intervalle sont alors:
borne inférieure a=c-r=-3-1=-4
borne supérieure b=c+r=-3+1=-2
et donc
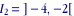
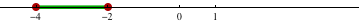
Intervalles fermés centrés
Considérons un intervalle fermé quelconque.
]a,b[ = {x ∈ R : a ≤x≤ b}
Recherchons le milieu (ou centre) c de cet intervalle. Il est obtenu par 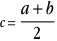 . .
Le rayon r de l'intervalle est alors la distance entre le centre et les "bords" (on parle de bornes) a et b de l'intervalle.
r est donc un réel strictement positif.
r=c-a

Plus simplement, c'est donc aussi la largeur (le diamètre) de l'intervalle divisé par 2.
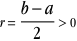

Exprimer l'appartenance d'un réel x à l'intervalle équivaut donc à dire que la distance entre x et le centre de l'intervalle doit être inférieure au rayon.
x ∈ [a,b]⇔ d(x,c)≤r⇔|x-c|≤r
On peut aussi obtenir cette relation de la manière suivante:
x ∈ [a,b]
⇔
a≤x≤b
⇔
0≤x-a et x-b≤0
⇔
0≤x-(c-r) et x-(c+r)≤0
⇔
-r≤x-c et x-c≤r
⇔
-r≤x-c≤r
⇔
|x-c|≤r
exemple 1: on considère l'intervalle fermé 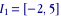
recherchons le centre et le rayon:
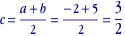
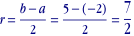
l'intervalle 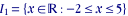 peut donc être défini de manière équivalente par peut donc être défini de manière équivalente par
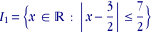

exemple 2: soit l'intervalle défini par 
la condition d'appartenance à l'intervalle étant |x-(-3)|≤1, nous voyons que le rayon est égal à 1 et le centre est égal à -3.
c=-3
r=1
les bornes de l'intervalle sont alors:
borne inférieure a=c-r=-3-1=-4
borne supérieure b=c+r=-3+1=-2
et donc
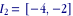
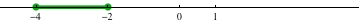
|












