|
Exercices résolus - 2 - Probabilités
EXPROBA21. Sur 10000 personnes d’un âge donné, il y a 400 cas de cancer du poumon.
Sur ces 10000 personnes, il y avait 6000 fumeurs dont 300 avaient le cancer du poumon. Quelle est la probabilité qu’une personne tirée au hasard
a) n’ait pas le cancer du poumon; 0.96
b) soit un fumeur cancéreux; 0.03
c) soit un fumeur si on sait qu’elle est cancéreuse? 0.75
EXPROBA22. Un homme a dans sa poche un trousseau de 6 clefs. Avant de rentrer chez lui, il constate qu’il a perdu une clef. Il doit ouvrir sa porte qui comporte deux serrures. Trouver
a) la probabilité qu’il sache ouvrir la porte; 2/3
b) la probabilité qu’il puisse ouvrir la porte avec les deux premières clefs qu’il essaie. 1/15
EXPROBA23. Dans une école, 40 étudiants ont Abel comme professeur, 60 ont Baudouin comme professeur.
10 étudiants d’Abel ont raté, et 12 élèves de Baudouin ont raté.
a) Un élève ayant raté est tiré au hasard. Quelle est la probabilité qu’il ait Abel comme professeur ?
b) Quelle est la probabilité qu’un élève quelconque ait raté et soit un élève de Baudouin?
c) Quelle est la probabilité qu’un élève choisi au hasard soit en échec ?
EXPROBA24. *Un test rapide pour détecter le cancer a été mis au point. Si un individu est cancéreux, il y a 95 chances sur 100 que le test réagisse positivement. Par contre, s'il est sain, il y a quand même 10 chances sur 100 que le test réagisse positivement. Dans une population donnée, on compte 18,5 % de réactions positives.
a) Trouver la proportion théorique de cancéreux dans cette population. 0.1
b) Si un individu est pris au hasard dans cette population, trouver la probabilité qu'il soit cancéreux et réagisse au test. 0.095
c) Si un individu choisi au hasard dans cette population a réagi positivement au test, trouver la probabilité que cet individu soit effectivement atteint du cancer. 0.513514
EXPROBA25. Un ranch possède 20 chevaux (6 blancs, 5 noirs et 9 gris) et une calèche prévue pour être tirée par 2 chevaux. Le cocher de la calèche choisit au hasard les 2 chevaux de l’attelage, parmi les 20 chevaux du ranch.
a) Calculer la probabilité des événements suivants :
A : « les 2 chevaux sont blancs », 0.0789474
B : « l’un des chevaux, au moins, est blanc », 0.521053
C : « les 2 chevaux sont de la même couleur ». 0.321053
b) Sachant que les deux chevaux de l’attelage sont de couleurs différentes, quelle est la probabilité pour que l’un soit blanc ? 0.651163
c) Des enfants effectuent un stage de 3 jours dans le ranch. le cocher organise alors, chaque jour, une promenade en calèche. Chaque jour, il choisit au hasard l’attelage.
Calculer la probabilité des événements suivants :
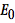 : « l’attelage n’est jamais unicolore », 0.312974 : « l’attelage n’est jamais unicolore », 0.312974
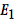 : « l’attelage est unicolore exactement une fois ». 0.443986 : « l’attelage est unicolore exactement une fois ». 0.443986
EXPROBA26. *Quelle est la probabilité d’amener le couple (1,1) au moins une fois en jetant 2 fois 2 dés?
EXPROBA27. Dans une classe, il y a 8 filles et 12 garçons. Dans une autre classe, 11 filles et 7 garçons. On tire une classe au sort (pile ou face) puis, dans la classe désignée, on choisit au hasard un élève. Une fille a-t-elle plus de chance d’être désignée qu’un garçon ? 0.505556
Solutions
|










