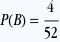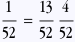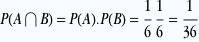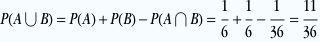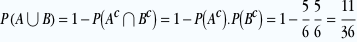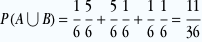|
Indépendance et incompatibilité
Evénements incompatibles
Deux événements A et B sont incompatibles ssi A∩B=Ø.
Autrement dit, deux événements sont incompatibles s’ils ne peuvent se réaliser en même temps.
exemple: On tire une carte au hasard d’un jeu de 52 cartes. Les événements A=”obtenir un coeur ♥️️” et B=”obtenir un pique ♠” sont bien incompatibles. Dès lors, P(A∩B)=0
Axiome 3 : si deux événements A et B sont incompatibles, alors P(A∪B)=P(A)+P(B)
exemple: On lance deux dés et on fait la somme des points obtenus. Soit A l’événement “obtenir une somme égale à 12” et B l’événement “obtenir une somme égale à 3”.
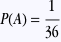 une seule manière d’obtenir 12: (6,6) une seule manière d’obtenir 12: (6,6)
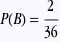 ici, deux manières: (1,2) et (2,1) ici, deux manières: (1,2) et (2,1)
De manière évidente, les deux événements sont incompatibles - la somme ne peut valoir à la fois 12 et 3..
Pour calculer P(A∪B), on utilise l’axiome 3.
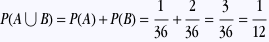
remarque: deux événements contraires sont forcément incompatibles
Evénements indépendants
Deux événements A et B sont indépendants ssi P(A∩B)=P(A) . P(B).
Autrement dit, deux événements sont indépendants si la réalisation de l'un ne dépend pas de la réalisation de l'autre.
exemple: On tire une carte au hasard d’un jeu de 52 cartes. Les événements A=”obtenir un coeur ♥️️” et B=”obtenir un as️” sont-ils indépendants? A votre avis...?
Calculons la probabilité des deux événements.
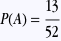 puisqu’il y a 13 coeurs dans le jeu de 52 cartes; puisqu’il y a 13 coeurs dans le jeu de 52 cartes;
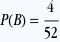 puisqu’il y a 4 as dans le jeu de 52 cartes. puisqu’il y a 4 as dans le jeu de 52 cartes.
Calculons maintenant la probabilité de l’intersection. A∩B est l’événement “obtenir un coeur et obtenir un as”, autrement dit “obtenir l’as de coeur”. Il n’y a qu’un seul as de coeur dans le jeu donc
 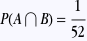
Pour vérifier si les événements sont indépendants, vérifions la définition:
P(A∩B)=P(A) . P(B)
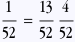
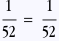
Donc oui, ils sont bien indépendants!
Pour comprendre de manière intuitive, posez-vous la question “je tire une carte; si on me dit que j’ai tiré un coeur, est-ce que du coup j’ai plus de chances (ou moins) d’avoir tiré un as ?” Non car il y a un as de coeur sur 13 coeurs (1/13), ce qui est la même proportion que d’as dans le jeu complet (4/52).
De même, si l’on me dit que j’ai tiré un as, ai-je plus de chances (ou moins) d’avoir tiré un coeur ? Non car il y a autant d’as de coeur que de pique, carreau ou trèfle.
En traduisant en formule, on peut aussi dire que P(A|B)=P(A) et P(B|A)=P(B)
Et si, en essayant de tricher, on ajoutait un deuxième as de coeur au jeu... ?*
Un dé est lancé six fois. Quelle est la probabilité d’obtenir le six lors du 1er lancer ou lors du 6ème lancer?
Soit A="obtenir 6 au 1er lancer" et B="obtenir 6 au 6ème lancer"
On cherche P(A∪B). Comme A et B ne sont pas incompatibles, on a
P(A∪B)=P(A)+P(B)-P(A∩B)
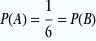 de manière évidente. de manière évidente.
Le résultat du 6ème lancer étant indépendant du 1er lancer, on a aussi
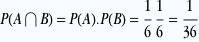
et on obtient 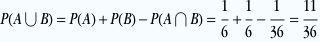
On pourrait aussi formuler le problème autrement en recherchant l’événement contraire: pour ne pas obtenir 6 au 1er lancer ou au 6ème lancer, il faudrait n’obtenir 6 ni au premier lancer ni au 6ème lancer.
C’est-a-dire que 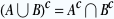 , donc ne pas obtenir 6 au 1er lancer et ne pas obtenir 6 au 6ème lancer. , donc ne pas obtenir 6 au 1er lancer et ne pas obtenir 6 au 6ème lancer.
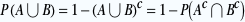
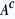 et et  étant indépendants, on a étant indépendants, on a
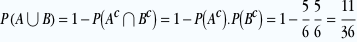 même résultat! (c’est rassurant..) même résultat! (c’est rassurant..)
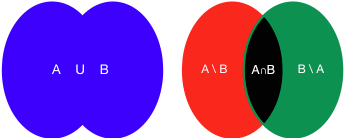
On peut aussi décomposer le problème en événements incompatibles: obtenir A ou B, c’est obtenir (A sans B) ou (B sans A) ou (A avec B)
ce qui donne
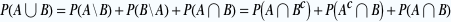
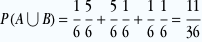 P P
Dans un paquet de 52 cartes bien mélangées, quelle est la probabilité que la carte du dessus soit l’as de pique ou que la carte du dessous soit l’as de pique ?
Soit A="la carte du dessus est l'as de pique" et B = “la carte du dessous est l’as de pique”
On demande de calculer P(A∪B).
A et B sont incompatibles, l’as de pique ne peut être au dessus et au dessous du paquet. Donc
P(A∪B)=P(A)+P(B) Axiome 3
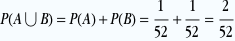
De plus, A et B sont clairement dépendants puisque si l’as de pique est au dessus du paquet, il ne peut pas être au dessous! Ce qui rend moins facile le calcul de l’événement contraire. Essayons quand même..
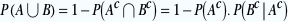
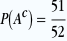 , c’est la probabilité que l’as de pique ne soit pas au dessus du paquet. , c’est la probabilité que l’as de pique ne soit pas au dessus du paquet.
Et 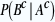 ? C’est la probabilité que l’as de pique soit au dessous du paquet sachant qu’il n’est pas au dessus. Donc, s’il n’est pas au dessus, il peut être à n’importe quelle des 51 autres positions et la probabilité qu’il ne soit pas au dessous est ? C’est la probabilité que l’as de pique soit au dessous du paquet sachant qu’il n’est pas au dessus. Donc, s’il n’est pas au dessus, il peut être à n’importe quelle des 51 autres positions et la probabilité qu’il ne soit pas au dessous est 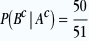 . .
Finalement, on obtient 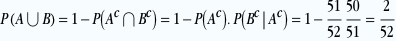
|